Forschungsgruppe
Formale Methoden und Theoretische Informatik

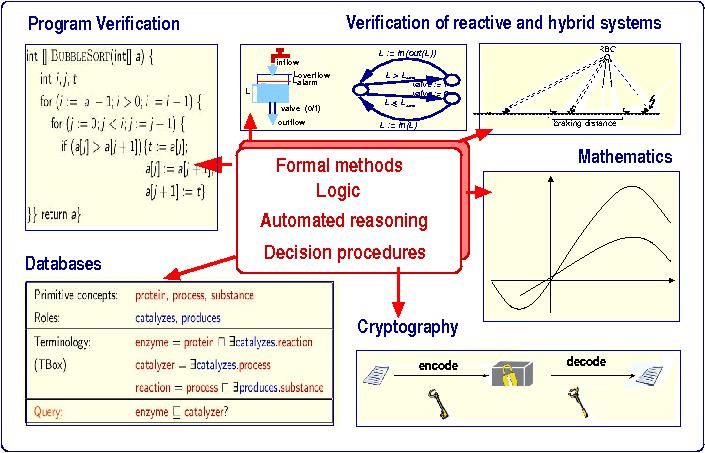
Der Forschungsschwerpunkt der Arbeitsgruppe ``Formale Methoden und Theoretische Informatik'' liegt in der Entwicklung von beweisbar korrekten Verfahren zur Verifikation und Analyse komplexer Systeme.

Das Ziel unserer Forschung ist es, Rahmenbedingungen zu identifizieren, unter denen effiziente automatische Verifikationsverfahren für komplexe Systeme existieren. Dabei untersuchen wir Möglichkeiten, Modularität in der Verifikation auf verschiedenen Ebenen auszunutzen, z.B.: Möglichkeiten för effizientes modulares Schließen in komplexen logischen Theorien, sowie Modellierung und modulare Verifikation von komplexen Systemen im Allgemeinen.

Unsere theoretischen Beiträge bilden die Basis für die Entwicklung von praktisch einsetzbaren Werkzeugen für die Verifikation sicherheitskritischer Systeme, insbesondere im Rahmen des SFB Transregio Projektes AVACS (Automatic Verification and Analysis of Complex Systems). Wir benutzen unsere Verfahren sowohl in der Programmverifikation, als auch um verschiedene Kontrollsysteme zu verifizieren (z.B. Funkkontroller für Zugsysteme, oder hybride Regelungsysteme für chemische Anlagen). Darüber hinaus wenden wir unsere Ansätze auch in der Kryptographie, bei Datenbanken oder in der Mathematik an.